
Concept explainers
The velocity of a rocket launched at
Answer to Problem 42P
The velocity of a rocket launched at
Explanation of Solution
Given info:
The latitude of the point of launch,
Velocity of the rocket with respect to the center of the Earth,
Formula used:
The velocity of the ground with respect to the ground
Here, r is the radius of the circular path traversed by the particle and T is the time taken for it to complete one rotation.
Calculation:
The point of launch is at a latitude
This is shown in the diagram below:
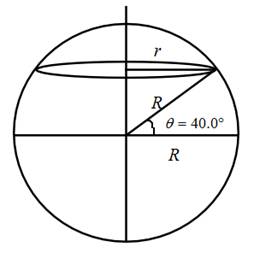
From the diagram, it can be seen that,
Here, R is the radius of the Earth, which has a value
Express the radius of the Earth in meters.
Calculate the value of r by substituting the values of R and
The Earth takes 24 h to complete one rotation. In the same time, the point on the ground completes its circular path of radius r .
Calculate the time T taken by the point on the ground to go once around the circular path of radius r in seconds.
Substitute the values of r and T in equation (1) and calculate the magnitude of the ground’s velocity relative to the center of the Earth.
The Earth rotates from west towards east. Hence, the point where the rocket is launched has a velocity
The rocket is launched with a speed of 11.0 km/s eastward with respect to the center of Earth.
Express the speed
The Ground rotates with a speed
The speed
Calculate the speed
If the rocket is launched at a point near the equator, the ground moves in a circular path equal to the radius of the Earth. Calculate the speed of the ground at the equator using equation (1) in the following form:
Substitute the given values in the above expression and calculate the velocity of the ground with respect to the center of Earth at equator.
The speed that needs to be imparted to the rocket at equator is the relative velocity of the rocket with respect to the ground.
The difference in the velocities of the rocket when launched at 40.0o latitude and at equator is given by,
Substitute the given values in the above expression:
Conclusion:
Thus, the velocity of a rocket launched at 40.0oNorth latitude along East, with respect to the ground is found to be
Want to see more full solutions like this?
Chapter 3 Solutions
Physics Fundamentals