
Introduction to mathematical programming
4th Edition
ISBN: 9780534359645
Author: Jeffrey B. Goldberg
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Question
Chapter 3, Problem 1RP
Program Plan Intro
Linear
- The linear programming(LP) is also known as linear optimization.
- Consider a mathematical model, and its requirements are used to represent by the linear relationships. The linear programming is the best method to achieve the best outcome of this mathematical model. The outcomes may be, maximum profit or lower cost.
- The linear optimization is also called as mathematical optimization because, it is a special case of mathematical programming.
- More formally, the LP is a technique for optimizing linear objective function subject to constraints of linear equality and linear inequality.
Expert Solution & Answer
Explanation of Solution
Linear programming for solving the problem:
Let
Then,
Explanation:
- The above programming statements are used to solve the beer and ale problem. In this there are two variables “x” and “y” used to represent the barrels of beer produced and barrels of ale produced respectively.
- The above statements give the formula to maximize the profit. Which is “5x + 2y”.
Solving LP graphically:
| Beer | Ale | Total | |
| Corn | 5lb | 2lb | 60 |
| Hopes | 2lb | 1lb | 25 |
Let
LP graph:
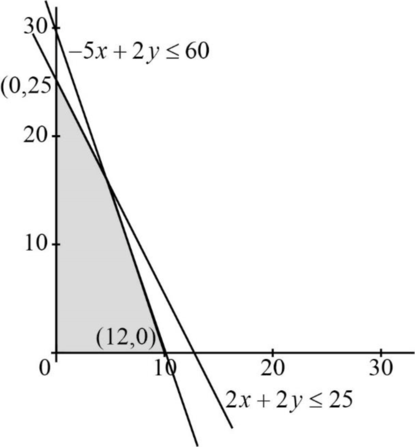
Vertices are,
Profit function:
The profit function at
The profit function at
The profit function at
The profit is maximized at the points,
That is 10 barrels of beer and 5 barrels of ale.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
Clyde Clerk is reviewing his firm’s expense reimbursement policies with the new salesperson, Trav Farr. “Our reimbursement policies depend on the situation. You see, first we determine if it is a local trip. If it is, we only pay mileage of 45 cents a mile. If the trip was a one-day trip, we pay mileage and then check the times of departure and return. To be reimbursed for breakfast, you must leave by 7:00 A.M., lunch by 11:00 A.M., and have dinner by 5:00 P.M. To receive reimbursement for breakfast, you must return later than 10:00 A.M., lunch later than 2:00 P.M., and have dinner by 7:00 P.M. On a trip lasting more than one day, we allow hotel, taxi, and airfare, as well as meal allowances. The same times apply for meal expenses.”
Draw a decision tree depicting the reimbursement policy in this Problem using LucidChart or Word document
3.
A company is considering opening warehouses in four cities: New York, Los Angeles, Chicago, and
Atlanta. Each warehouse can ship 100 units per week. The weekly fixed cost of keeping each warehouse
open is $400 for New York, $500 for Los Angeles, $300 for Chicago, and $150 for Atlanta. Region 1 of
the country requires 80 units per week, region 2 requires 70 units per week, and region 3 requires 40
units per week. The costs (including production and shipping costs) of sending one unit from a plant
to a region are shown in Table 3. We want to meet weekly demands at minimum cost, subject to the
preceding information and the following restrictions:
1.
If the New York warehouse is opened, then the Los Angeles warehouse must be opened.
2.
At most two warehouses can be opened.
3.
Either the Atlanta or the Los Angeles warehouse must be opened.
Formulate an IP that can be used to minimize the weekly costs of meeting demand.
Table 3
To ($)
From
Region 1
Region 2
Region 3
New York
20
40
50
Los…
Q1: Reddy Mikks produces both interior and exterior paints from two raw materials, M1 and
M2. The following table provides the basic data of the problem:
Tons of raw material per ton of
Maximum daily
availability (tons)
Exterior paint
Interior paint
Raw material, M1
6
4
24
Raw material, M2
1
2
6
Profit per ton ($1000)
5
4
The daily demand for interior paint cannot exceed that for exterior paint by more than 1 ton. Also,
the maximum daily demand for interior paint is 2 tons. Reddy Mikks wants to determine the
optimum (best) product mix of interior and exterior paints that maximizes the total daily profit.
Give the mathematical formula of only the demand constraint? (15 mark)
Note for form's designer: design the answer to be as a short paragraph.
إجابتك
Chapter 3 Solutions
Introduction to mathematical programming
Ch. 3.1 - Prob. 1PCh. 3.1 - Prob. 2PCh. 3.1 - Prob. 3PCh. 3.1 - Prob. 4PCh. 3.1 - Prob. 5PCh. 3.2 - Prob. 1PCh. 3.2 - Prob. 2PCh. 3.2 - Prob. 3PCh. 3.2 - Prob. 4PCh. 3.2 - Prob. 5P
Ch. 3.2 - Prob. 6PCh. 3.3 - Prob. 1PCh. 3.3 - Prob. 2PCh. 3.3 - Prob. 3PCh. 3.3 - Prob. 4PCh. 3.3 - Prob. 5PCh. 3.3 - Prob. 6PCh. 3.3 - Prob. 7PCh. 3.3 - Prob. 8PCh. 3.3 - Prob. 9PCh. 3.3 - Prob. 10PCh. 3.4 - Prob. 1PCh. 3.4 - Prob. 2PCh. 3.4 - Prob. 3PCh. 3.4 - Prob. 4PCh. 3.5 - Prob. 1PCh. 3.5 - Prob. 2PCh. 3.5 - Prob. 3PCh. 3.5 - Prob. 4PCh. 3.5 - Prob. 5PCh. 3.5 - Prob. 6PCh. 3.5 - Prob. 7PCh. 3.6 - Prob. 1PCh. 3.6 - Prob. 2PCh. 3.6 - Prob. 3PCh. 3.6 - Prob. 4PCh. 3.6 - Prob. 5PCh. 3.7 - Prob. 1PCh. 3.8 - Prob. 1PCh. 3.8 - Prob. 2PCh. 3.8 - Prob. 3PCh. 3.8 - Prob. 4PCh. 3.8 - Prob. 5PCh. 3.8 - Prob. 6PCh. 3.8 - Prob. 7PCh. 3.8 - Prob. 8PCh. 3.8 - Prob. 9PCh. 3.8 - Prob. 10PCh. 3.8 - Prob. 11PCh. 3.8 - Prob. 12PCh. 3.8 - Prob. 13PCh. 3.8 - Prob. 14PCh. 3.9 - Prob. 1PCh. 3.9 - Prob. 2PCh. 3.9 - Prob. 3PCh. 3.9 - Prob. 4PCh. 3.9 - Prob. 5PCh. 3.9 - Prob. 6PCh. 3.9 - Prob. 7PCh. 3.9 - Prob. 8PCh. 3.9 - Prob. 9PCh. 3.9 - Prob. 10PCh. 3.9 - Prob. 11PCh. 3.9 - Prob. 12PCh. 3.9 - Prob. 13PCh. 3.9 - Prob. 14PCh. 3.10 - Prob. 1PCh. 3.10 - Prob. 2PCh. 3.10 - Prob. 3PCh. 3.10 - Prob. 4PCh. 3.10 - Prob. 5PCh. 3.10 - Prob. 6PCh. 3.10 - Prob. 7PCh. 3.10 - Prob. 8PCh. 3.10 - Prob. 9PCh. 3.11 - Prob. 1PCh. 3.11 - Show that Fincos objective function may also be...Ch. 3.11 - Prob. 3PCh. 3.11 - Prob. 4PCh. 3.11 - Prob. 7PCh. 3.11 - Prob. 8PCh. 3.11 - Prob. 9PCh. 3.12 - Prob. 2PCh. 3.12 - Prob. 3PCh. 3.12 - Prob. 4PCh. 3 - Prob. 1RPCh. 3 - Prob. 2RPCh. 3 - Prob. 3RPCh. 3 - Prob. 4RPCh. 3 - Prob. 5RPCh. 3 - Prob. 6RPCh. 3 - Prob. 7RPCh. 3 - Prob. 8RPCh. 3 - Prob. 9RPCh. 3 - Prob. 10RPCh. 3 - Prob. 11RPCh. 3 - Prob. 12RPCh. 3 - Prob. 13RPCh. 3 - Prob. 14RPCh. 3 - Prob. 15RPCh. 3 - Prob. 16RPCh. 3 - Prob. 17RPCh. 3 - Prob. 18RPCh. 3 - Prob. 19RPCh. 3 - Prob. 20RPCh. 3 - Prob. 21RPCh. 3 - Prob. 22RPCh. 3 - Prob. 23RPCh. 3 - Prob. 24RPCh. 3 - Prob. 25RPCh. 3 - Prob. 26RPCh. 3 - Prob. 27RPCh. 3 - Prob. 28RPCh. 3 - Prob. 29RPCh. 3 - Prob. 30RPCh. 3 - Prob. 31RPCh. 3 - Prob. 32RPCh. 3 - Prob. 33RPCh. 3 - Prob. 34RPCh. 3 - Prob. 35RPCh. 3 - Prob. 36RPCh. 3 - Prob. 37RPCh. 3 - Prob. 38RPCh. 3 - Prob. 39RPCh. 3 - Prob. 40RPCh. 3 - Prob. 41RPCh. 3 - Prob. 42RPCh. 3 - Prob. 43RPCh. 3 - Prob. 44RPCh. 3 - Prob. 45RPCh. 3 - Prob. 46RPCh. 3 - Prob. 47RPCh. 3 - Prob. 48RPCh. 3 - Prob. 49RPCh. 3 - Prob. 50RPCh. 3 - Prob. 51RPCh. 3 - Prob. 52RPCh. 3 - Prob. 53RPCh. 3 - Prob. 54RPCh. 3 - Prob. 56RPCh. 3 - Prob. 57RPCh. 3 - Prob. 58RPCh. 3 - Prob. 59RPCh. 3 - Prob. 60RPCh. 3 - Prob. 61RPCh. 3 - Prob. 62RPCh. 3 - Prob. 63RP
Knowledge Booster
Similar questions
- Andalus Furniture Company has two manufacturing plants, one at Aynor and another at Spartanburg. The cost in dollars of producing a kitchen chair at each of the two plants is given here. Aynor: Cost = 65Q1 + 5Q12 + 96Spartanburg: Cost = 21Q2 + 3Q22 + 147 Where Q1 = number of chairs produced at Aynor Q2= number of chairs produced at Spartanburg Andalus needs to manufacture a total of 50 kitchen chairs to meet an order just received. How many chairs should be made at Aynor and how many should be made at Spartanburg in order to minimize total production cost? Can you use Excel to formulate and Solver to solve.arrow_forwardDamla has graduated from an MBA program recently. She has $1,200 dollar on hand, to invest for several alternatives. With the help her mathematical modelling ideas, she want to invest her money in several financial alternatives. She may invest her money on hand in bonds and loans. Each dollar invested in bonds yields $0.18 profit, and each dollar invested in a loan yields $0.13 profit. At least 32% of all money invested must be in bonds, and at least $380 must be in loans. a) Formulate an LP that can be used to maximize total profit earned from Damla’s investment. b) Solve the problem in IBM ILOG CPLEX Optimization Studio and submit your optimal solution. c) Solve the problem graphically. Verify your solution with the optimal solution that you have found in part (b)arrow_forwardPortfolio manager Max Gaines needs to develop an investment portfolio for his clients who are willing to accept a moderate amount of risk. His task is to determine the proportion of the portfolio to invest in each of the five mutual funds listed below so that the portfolio maximizes the expected return but provides an annual return of no less than 3%. for each of the following scenarios. Annual Returns (Planning Scenarios): mutual fund yr 1 yr 2 yr 3 yr 4 international stock 22.37 26.73 6.46 -3.19 low-cap blend 14.88 18.61 10.52 5.25 mid-cap blend 19.45 18.04 5.91 -1.94 small-cap blend 13.79 11.33 -2.07 6.85 intermediate bond 7.29 8.05 9.18 3.92 Formulate the appropriate linear program for this situation. (state the objective function, the decision variables, and the constraints)arrow_forward
- A company owns the same asset in a ASIAN plant and in a UK plant . It has B $2,000,000 and a salvage value of 20% of B . For tax depreciation purposes, ASIA allows a straight line write-off over 5 years, while the UK allows SL write-off over 8 years. The general managers of the two plants want to know the difference in the depreciation amount for year 5.arrow_forwardThe Livewright Medical Supplies Company has a total of 12 salespeople it wants to assign to three regions-the South, the East, and the Midwest. A salesperson in the South earns $600 in profit per month for the company, a salesperson in the East earns $540, and a salesperson in the Midwest earns $375. The southern region can have a maximum assignment of five sales- people. The company has a total of $750 per day available for expenses for all 12 salespeople. A salesperson in the South has average expenses of $80 per day, a salesperson in the East has average expenses of $70 per day, and a salesperson in the Midwest has average daily expenses of $50. The company wants to determine the number of salespeople to assign to each region to maximize profit. a. Formulate an integer programming model for this problem. b. Solve this model by using the computer.arrow_forwardRidgley Custom Metal Products (RCMP) must purchase a new tube bender. RCMP's MARR is 12 percent. RCMP can forecast demand for its products for only 4 years in advance. The salvage value after 4 years is $50,000 for model T, $85,000 for model A and $75,000 for model X. Using the study period method, which of the three alternatives is best? Salvage Value $50.000 Yearly Net Savings $55.000 $50.000 $65.000 Model First Cost Economic Life $100,000 $140,000 $190,000 4 years 4 years A $85,000 $75,000 4 years Click the icon to view the table of compound interest factors for discrete compounding periods when i= 12%. The present worth of Model T is $. The present worth of Model A is $ The present worth of Model X is $. Model V is the better choice to buy. (Round to the nearest cent as needed.)arrow_forward
- The Callaghan family owns 410 acres of farmland in Co. Cork on which they grow wheat and oats. Each acre of wheat costs €105 to plant, cultivate, and harvest; each acre of oats costs €210. The Bradleys have a budget of €52,500 for next year. The government limits the number of acres of oats that can be planted to 100. The profit from each acre of wheat is €300; the profit from each acre of oats is €520. The Callaghans want to know how many acres of each crop to plant in order to maximize their profit. ii. Formulate a linear programming model for this problem.arrow_forwardVandelay Industries has 275 sales reps in order to sell its latex products, each to be assigned to one of four marketing teams. If the first team is to have four times as many members as the second team and the third team is to have five times as many members as the fourth team, how can the members be distributed among the teams?arrow_forwardABC Company produces three electrical products—blenders, choppers, and toasters. The manufacturer has a maximum daily production budget of RM2000 and a maximum of 660 hours of labor. Maximum daily customer demand is for 200 blenders, 300 choppers, and 150 toasters. The unit profit for blender is RM8, choppers, RM10, and toaster, RM7. The company desires to know the optimal product mix that will maximize profit. These products have the following resource requirements as shown in Table 1. Based on the report, answer the following questions and justify all your answers. Formulate the LP model for the above case study. Suppose that the company would like to increase the profit of the toasters to RM9 per unit without affecting the optimum number of products to be produced based on earlier conditions. Based on the Sensitivity Report, advise the company if this can be accomplished and justify your answer. If this can be done, what would be the company’s profit based on new pricing. The…arrow_forward
- ABC Company produces three electrical products—blenders, choppers, and toasters. The manufacturer has a maximum daily production budget of RM2000 and a maximum of 660 hours of labor. Maximum daily customer demand is for 200 blenders, 300 choppers, and 150 toasters. The unit profit for blender is RM8, choppers, RM10, and toaster, RM7. The company desires to know the optimal product mix that will maximize profit. These products have the following resource requirements as shown in Table 1. Based on the report, answer the following questions and justify all your answers. Formulate the LP model for the above case study. Optimize the Company ABC production using linear programming simplex method. Suppose that the company would like to increase the profit of the toasters to RM9 per unit without affecting the optimum number of products to be produced based on earlier conditions. Based on the Sensitivity Report, advise the company if this can be accomplished and justify your answer. If this…arrow_forwardMr. Ramkunwar has divided his property in three parts in the ratio of 13:12:11 for his sons Jugal, Chandan and Raunak. The eldest (Jugal) to get maximum share and the youngest (Raunak) to get minimum share. Find the share of each son if total valuation of prperty is 14,40,000.arrow_forwardSteelco manufactures two types of steel at three different steel mills. During a given month, each steel mill has 200 hours of blast furnace time available. Because of differences in the furnaces at each mill, the time and cost to produce a ton of steel differs for each mill. The time and cost for each mill are shown in the table below. Each month, Steelco must manufacture at least 500 tons of steel 1 and 600 tons of steel 2. Formulate an LP to minimize the cost of manufacturing the desired steel.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole
Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole

Operations Research : Applications and Algorithms
Computer Science
ISBN:9780534380588
Author:Wayne L. Winston
Publisher:Brooks Cole