
Concept explainers
(a)
The
(a)
Answer to Problem 11.29P
The
Explanation of Solution
Write the expression to find the Hamiltonian matric for a spinning charge particle in a magnetic field
Here,
Write the expression for appropriate spin matrix
Where,
Given, the total magnetic field
Where,
Solving equation (I),
Substitute equation (II) in the above equation,
Solving further,
Conclusion:
Thus, the
(b)
Show that
(b)
Answer to Problem 11.29P
It has been proved that
Explanation of Solution
Write the time-dependent Schrodinger equation
Given,
Thus,
Substitute the above relations in equation (IV)
From part (a),
Thus,
Hence proved.
Conclusion:
It has been proved that
(c)
Whether the general solution for
(c)
Answer to Problem 11.29P
It has been proved that the general solution for
Explanation of Solution
From part (b),
Using the above relations,
Differentiate
Rewrite the above equation in the form of second order differential equation,
Solving the terms inside the bracket,
Substitute the above relation in equation (V)
The characteristic equation is
Solving the above quadratic equation,
Where,
The general solution
The general solution
For the initial condition,
From part (b),
Substitute
Substitute equation (IX) and (X) in (VII)
And
Hence proved.
Conclusion:
It has been proved that the general solution for
(d)
The probability of a transition to spin down, as a function of time.
(d)
Answer to Problem 11.29P
The probability of a transition to spin down, as a function of time is
Explanation of Solution
Write the expression to find the probability of transition to spin down
Given,
Substitute
Now, the probability of a transition to spin down is
Conclusion:
Thus, the probability of a transition to spin down, as a function of time is
(e)
Sketch the resonance curve,
(e)
Answer to Problem 11.29P
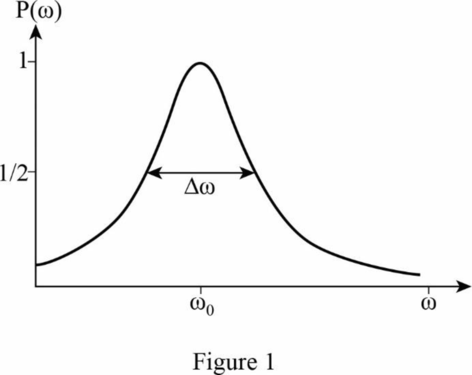
The resonance curve,
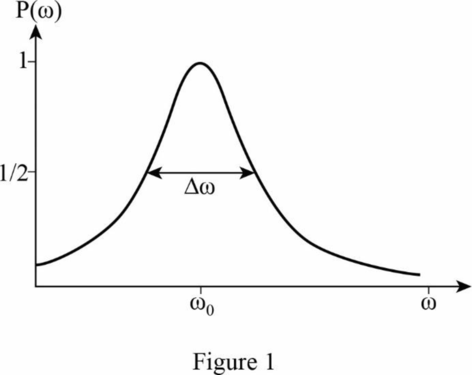
the full width at half maximum is
Explanation of Solution
Given,
Taking square root on both sides,
Thus, the full width at half maximum,
Conclusion:
The resonance curve,
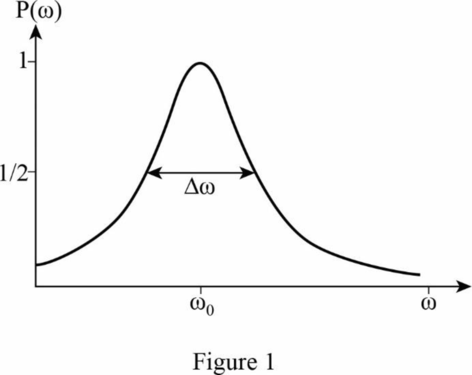
the full width at half maximum is
(f)
The resonant frequency in a nuclear magnetic resonance experiment and the width of the resonance curve.
(f)
Answer to Problem 11.29P
The resonant frequency in a nuclear magnetic resonance experiment is
Explanation of Solution
Compare Equation 4.156 and 7.89, the gyro-magnetic ratio for a proton is
Where,
Write the expression to find the resonant frequency
Where,
Substitute equation (XI) in the above equation,
Substitute
Write the expression to find the width of the resonance curve
Where,
Thus, the above equation becomes,
Substitute
Conclusion:
Thus, the resonant frequency in a nuclear magnetic resonance experiment is
Want to see more full solutions like this?
Chapter 11 Solutions
Introduction To Quantum Mechanics
- F.j = (-e)(-v,k) × (B,i + B.k) ev Bzj. Solving for B gives F. Br 8.50x10 16 N = 1.13 T. Therefore B = 1.13 Ti – 0.772 Tk. The magnitude o A group of particles is traveling in a magnetic field of unknown magnitude and direction. You observe that a proton moving at 1.70 km/s in the +x-direction experiences a force of 2.10x10-16 N in the +y- direction, and an electron moving at 4.70 km/s in the eve (1.60x10 19 C)(4700 m/s) is B = VB? + B = (1.13 T)² + (-0.772 T)² = 1.37 T. -z-direction experiences a force of 8.50x10-16 N in the +y-direction. Part B For related problem-solving tips and strategies, you may want to view a Video Tutor Solution of Magnetic force on a proton. What is the direction of the magnetic field? (in the xz-plane) Express your answer in degrees. 0 = 60.59 ° from the -z-direction to the +x-direction Submit Previous Answers Request Answer X Incorrect; Try Again; 9 attempts remainingarrow_forwardTwo electrons at fixed positions on the z-axis have a magnetic dipole- dipole interaction (energy) E = A(s1 · $2 - 3s1z822), where s; = being Pauli's spin matrix, A = constant. oi, ai (a) Express E/A in terms of the total spin operator S = s1 + $2- (b) State the eigenvalues of E/A and their degeneracy (statistical weights).arrow_forwardThe potential energy of a magnetic moment in an external magnetic field is given by U = -u-B. The magnetic moment associated with the spin of an electron is 5.79 x 10-5 eV/T. Calculate the difference in energy between the two possible orientations of an electron in energy in a magnetic field B = (0.8 T) k. Answer in units of eV. %3D %3D If these electrons are bombarded with photons of energy equal to this energy difference, "spin flip" transitions can be induced. Find the wavelength of the photons needed for such transitions. (This phenomenon is called electron spin resonance.) Answer in units of cm.arrow_forward
- Consider a hydrogen atom in which an electron is revolving in n=1 orbit with 6.57x105 revolutions per second. Calculate the magnetic moment of the electron. Answer Choices: a. 9.2x10-24 A - m? b. 6.5x10-24 A m? c. 5.5x10-* A -m? d. 7.4x10-24 A m?arrow_forwardFor a 5p electron in an external magnetic field of 4.70 ✕ 10−3 T, find the following. (a) the current (in A) associated with the orbital angular momentum (b) the maximum torque (in N · m)arrow_forward6. A solid at temperature is placed in an external magnetic field B = 1 Tesla = 1 × 10¹ gauss. The solid contains weakly interacting paramagnetic atoms of spin 1/2, so that the energy of each atom is ±μB. a. If the magnetic moment is equal to one Bohr magneton, i.e., μ = h x 1.4 MHz/gauss, below what temperature must one cool the solid so that more than 75% of the atoms are polarized with their spins parallel to the external magnetic field? b. Suppose that one considered instead a solid which is free of paramagnetic atoms but contains many protons (e.g., paraffin). Each proton has spin 1/2 and a magnetic moment µp = h x 2.1 kHz/gauss. At the same temperature as you determined in part a., what fraction of protons will have their spins aligned parallel to the external magnetic field?arrow_forward
- The force on a magnetic moment z in a nonuniform magnetic field Bz is given by Fz=zdBzdz If a beam of silver atoms travels a horizontal distance of 1 m through such a field and each atom has a speed of 100 m/s, how strong must the field gradient dBz/dz be in order to deflect the beam 1 mm?arrow_forwardWhat is the magnitude of the spin momentum of an electron? (Express you answer in terms of h.)arrow_forwardA mystery particle enters the region between the plates of a Thomson apparatus as shown in Figure 4.6. The deflection angle θ is measured to be 0.20 radians (downwards) for this particle when V = 2000 V, ℓ = 10.0 cm, and d = 2.00 cm. If a perpendicular magnetic field of magnitude 4.57 × 10−2 T is applied simultaneously with the electric field, the particle passes through the plates without deflection. (a) Find q/m for this particle. (b) Identify the particle. (c) Find the horizontal speed with which the particle entered the plates. (d) Must we use relativistic mechanics for this particle?arrow_forward
- While studying the spectrum of a gas cloud in space, an astronomer magnifies a spectral line that results from a transition from a to an s state. She finds that the line at 575.050 nm has actually split into three lines, with adjacent lines 4.30 x 10-2 nm apart, indicating that the gas is in an external magnetic field. (Ignore effects due to electron spin.) state What is the strength of the external magnetic field? a) O 2.79 T b) 2.98T c) 2.67 T d) 3.08 T e) 3.05 Tarrow_forwardA magnetic field is applied to a freely floating uniform iron sphere with radius R = 2.00 mm. The sphere initially had no net magnetic moment, but the field aligns 12% of the magnetic moments of the atoms (that is, 12% of the magnetic moments of the loosely bound electrons in the sphere, with one such electron per atom). The magnetic moment of those aligned electrons is the sphere’s intrinsic magnetic moment .What is the sphere’s resulting angular speed v?arrow_forwardEach of 2N electrons (mass m) is free to move along the x-axis. The potential energy for each electron is U(x) = kx², where k is a positive constant. The electric and magnetic interactions between electrons are ignored. Use the exclusion principle and find the minimum energy of the system of 2N electrons.arrow_forward
 Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning
Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax



