Let Vn be the set of connected graphs having n edges, vertex set [n], and exactly one cycle. Form a graph Gn whose vertex set is Vn. Include {gn, hn} as an edge of Gn if and only if gn and hn differ by two edges, i.e. you can obtain one from the other by moving a single edge. Tell us anything you can about the graph Gn. For example, (a) How many vertices does it have? (b) Is it regular (i.e. all vertices the same degree)? (c) Is it connected? (d) What is its diameter?
Let Vn be the set of connected graphs having n edges, vertex set [n], and exactly one cycle. Form a graph Gn whose vertex set is Vn. Include {gn, hn} as an edge of Gn if and only if gn and hn differ by two edges, i.e. you can obtain one from the other by moving a single edge. Tell us anything you can about the graph Gn. For example,
(a) How many vertices does it have?
(b) Is it regular (i.e. all vertices the same degree)?
(c) Is it connected?
(d) What is its diameter?
Given
Let be the set of connected graphs having n edges, vertex set [n], and exactly one cycle. Form a graph whose vertex set is . Include as an edge of if and only if and differ by two edges, i.e. you can obtain one from the other by moving a single edge. Tell us anything you can about the graph .
Graph
Related graph example
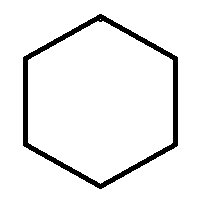
Here number of vertices =number of edges.
Then only possible without multi edge with is cycle.
Thus the graph is cycle.
Step by step
Solved in 3 steps with 1 images







